Evaluating the Impact of CT Scanning Parameters on Dose Calculations by the Treatment Planning System in External Beam Radiation Therapy

   

Barrington A Brevitt^1*, Edwin Ges Suarez², Rafael A Miller Clemente³ and Mitko Voutchkov¹

Received: November 03, 2021 | Published: November 28, 2021

Copyright^© 2021 genesis pub by Brevitt BA, et al. CC BY NC-ND 4.0 DEED. This is an open-access article distributed under the terms of the Creative Commons Attribution-NonCommercial-No Derivatives 4.0 International License., This allows others distribute, remix, tweak, and build upon the work, even commercially, as long as they credit the authors for the original creation.

DOI: https://doi.org/10.52793/JCTR.2021.1(1)-08

Abstract

This study sought to evaluate scanning parameters for Computed Tomography (CT) simulations and its impact on dose calculation by a treatment planning systems. A Computerized Imaging Reference System (CIRS) electron density phantom was scanned with a GE multi-detector scanner to acquire 1.25 mm slices in helical mode. Evaluations were done with the standard image reconstruction using a circular region of interest (ROI) from the measuring tool of the workstation software. Radiation therapy plans were prepared using the Eclipse Treatment Planning System (TPS) and an analysis of the influence of the scanning parameters over dose calculation was done. Scanning parameters can affect the dose calculation resulting in deviations between the TPS and Hounsfield Unit- relative electron density (HU-EDr) calibration curve. Such deviations may lead to uncertainties in the calculation of output dose in the radiotherapy plan. Changes in kilo-voltage peak (kVp) had a direct impact on the HU measured for each tissue-equivalent insert. The effects of different tube voltages on the HU for various tissue substitutes in the phantom, and their dosimetric impact on dose calculation in TPS is due to variations in the HU-EDr calibration curve. The technical factors selected for scanning has a direct impact on the HU value obtained from the scan data. This in turn affects HU-EDr calibration and radiation therapy dose calculations.

Keywords

Hounsfield units; Relative electron density; Monte carlo; Linear attenuation; Tissue maximum ratio (TMR)

Introduction

The quality of Computed Tomography (CT) images influence the recognition and delineation of target volumes and the surrounding organs at risk (OARs). Substandard image quality may result in improper delineation of the target volume and OARs by omission of the target or over-inclusion of a portion of normal organ volumes. Thus, it is essential to evaluate the image quality of CT scanners used for simulation of radiotherapy patients. The accuracy of dose calculation by the radiotherapy Treatment Planning System (TPS), takes into account the effect of tissue inhomogeneities based on CT data and the calibration of CT Hounsfield Unit (HU) and Relative Electron Density (ED_r) curves. CT number or HU provides information on the attenuation characteristics of X-ray beam in a particular volume element in the patients’ body with respect to that of water at a specific kilo-voltage peak (kVp).

The images obtained from CT can be used in radiation oncology as a basis for dose distribution when treatment plans are being prepared for internal or external radiation therapy. As x-rays traverse the patients’ body, they interact with tissue of varying densities giving rise to Compton and Photoelectric scattering. These interactions are dependent on the photon energy; the effective atomic number and the electron density of the medium. Photons ranging in energies of 0.3-2 MeV undergo the Compton Effect and those that are less or in excess of this energy range are involved in the Photoelectric Effect or other photon-matter interactions respectively. These scattered photon energies give rise to photon fluence which can be used to estimate the electron densities (ED) of tissue along the path traversed by the beam. Table 1 highlights the various inhomogeneities encountered by the treatment beam as it traverses the patient’s body to the target volume. These differences create a heterogeneous environment requiring precise and accurate treatment planning and dose delivery.

Tissue	Typical HU	Typical Thickness (cm)	EDr	Product of t and (EDr-1)
Lung	-740	8	0.26	-5.92
Fat	-50	4	0.95	0.20
Liver	50	8	1.05	0.40
Rib	600	1	1.34	0.34
Humerus	700	2.5	1.39	0.98
Cranium	900	1.5	1.51	0.77

Table 1: Typical inhomogeneities encountered in treatment planning and changes in water equivalent thickness caused by inhomogeneity.

Electron Density (ED) is defined as the number of electrons contained by tissue of specific density expressed in electrons/cm³.  When the electron density of tissue (ED_t) is compared to the electron density of water (ED_w) it results in a ratio referred to as the relative electron density (ED_r).  It is known that a relationship exists between ED_r and the HU generated for each pixel of a CT scan [1]. The HU is generated for each pixel of the CT cross-sectional image resulting from the linear attenuation of x-rays as they interact with different tissue densities within the body. HU is the difference of the linear attenuation of tissue within a pixel and the linear attenuation of water within a similar pixel, and is calculated from:

Where: (µ_t) is the linear attenuation of tissue and (µ_w) is the linear attenuation of water. Attenuation coefficients depend on electron density, atomic number (Z) and the quality of the beam used for the scan [2].

Computed tomography in radiation therapy has three applications; it is used for the acquisition of patient images and tumors contours; it is employed to evaluate the results of treatment and for obtaining density information concerning the patient to improve the accuracy of dose calculations. The construction of a CT scanner generates systematic errors due to beam hardening and the detection of scattered radiation. In early generation scanners, these errors usually manifest as an increasing density towards the centre of the image known as the cupping effect [3]. In later generation scanners corrections are done by a process of linearizing the x-ray transmission data.

Scanners generate HU which are physical quantities allowing universal characterization of human tissue for diagnostic purposes and heterogeneity corrections in radiation therapy planning. The polychromatic x-ray source used in CT coupled with a broad energy response detector prevents the separate detection of primary and scattered radiation. Scanners are constructed to reduce the degree of scattering reaching the detector; however, for scattered rays detected they create errors in the determination of the linear attenuation coefficient. In radiation therapy planning, a patient’s body is compared to water of variable effective densities, corresponding to electron density for high energy photons or stopping power ratio for charged particles. As cancer treatment and technology evolves, the use of simulation CTs is becoming more prevalent, where radiation is utilized as an assortment of particles interacting with tissue of known composition and used for Monte Carlo (MC) calculations. For patient dose calculations the TPS uses MC functions to convert HU to effective densities of interest. For other analytical dose calculation algorithms e.g. AAA, the TPS uses HU-electron density calibration curves for this conversion. In algorithms such as Acuros XB, the TPS uses the HU value-density calibration curves to convert HU to the material composition. The HUs are converted to ED that is automatically converted to interaction-specific effective densities using invariant associations [4]. This proves the importance of accurate representation of ED within the TPS and the scanning system, as inaccuracies can result in calculation errors.

Methodology

Scans of a Computerized Imaging Reference System (CIRS) electron density phantom (model 062M) were acquired with a GE Optima 16 slice multi-detector (MD) scanner with the scanning parameters outlined in Table 2. The distribution of the tissue-equivalent inserts within the phantom is shown in Figure 1, while Table 3 outlines the different densities of the inserts used to acquire HU and standard deviation (SD) measurements.

Figure 1: Distribution of tissue-equivalent inserts in CIRS phantom.

The phantom was aligned using external wall and ceiling lasers as seen in Figure 2 and the first set of scans were acquired at tube voltages of 80, 100, 120 and 140 kVp respectively, with the tube current set at 400 mA.  The second set of scans was acquired with the tube voltage set at 120 kVp while varying the tube current. The values used were 100, 200, 300, 400 and 440 mA respectively.
 

Slice thickness	1.25 mm
Window Width / Window Level	350/40
Pitch	0.938:1
Tilt	00
Recon Type	Standard
DFOV	41.8 cm
Matrix size	512
SFOV	Large Head
Scan Type	Helical

Table 2: Scan acquisition parameters.

Figure 2: Set-up of the phantom using external lasers.

Three scans were done at each kVp and mA setting to account for uncertainties in measurements. The measuring tool on the view station was used to select a circular ROI (444.47 mm²) with a diameter of 24 mm to evaluate the mean Hounsfield Unit and standard deviation of each tissue-equivalent insert for each tube voltage and current setting. Calibration curves were compared to theoretical curves calculated by Varian, which was pre-set in the Eclipse TPS and were considered as a reference 5 [5].              

HU < 100: ED_r = 1 + (1.001 x HU)                                                         (2)

HU > 100: ED_r = 1.052 + (0.00048 x HU)                                               (3)

The scan images were transferred to the Eclipse TPS version 15.0 and processed using the contouring tool. Subsequent to image transfer a fusion was done and the recommended quality assurance tests were performed as seen in Figure 3. The fused images were then employed to conduct typical radiotherapy planning techniques such as 3-Dimensional Radiation Therapy (3DRT) and Volumetric Modulated Arc Therapy (VMAT) which is an inverse planning technique as shown in Figure 7 and Figure 8. This was done to evaluate the influence of the ED_r assumed by the TPS in the dose calculation process.

Tissue  Equivalent Material (density plugs)	Physical Density (g/cc)	Electron Density (x 1023 electrons/cc)	EDr (relative to water)
Lung Inhale	0.205	0.668	0.200
Lung Exhale	0.507	1.658	0.496
Adipose	0.96	3.171	0.949
Breast (50% gland/ 50% Adipose)	0.99	3.261	0.976
Muscle	1.06	3.483	1.043
Liver	1.07	3.516	1.052
Solid Trabecular Bone (200 mg/cc HA)	1.16	3.730	1.117
Solid Dense Bone (800 mg/cc HA)	1.53	4.862	1.456

Table 3: Phantom Specifications.

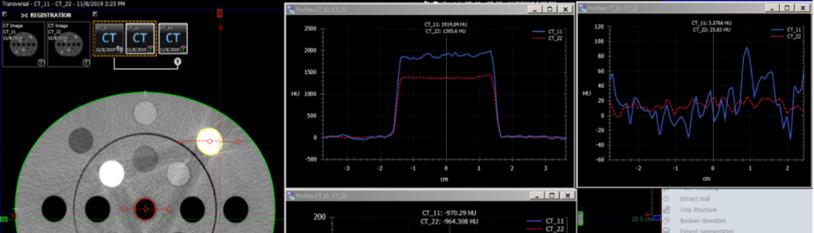
Figure 3: Profile of Fused Images at 80 and 140 kVp.

Results

It was found as illustrated in Table 4 that changes in kVp had a direct impact on the HU measured for each tissue-equivalent insert. Changes in kVp and mA also had effects on the ED_r of the tissue inserts. HU analysis by the TPS of imported images, yielded results consistent with those obtained from the scanner software before images were imported. Figure 3 shows profiles generated when image fusion was done with phantom images obtained at 80 kVp and 140 kVp. This analysis highlighted a disparity with the HU measured for high density material. A direct relationship between kVp and ED_r was observed, as increases in the tube voltage resulted in a corresponding rise in ED_r. This relationship was not apparent with tube current. As the mA increased there were negligible changes in ED_r producing a uniform curve as shown in Figure 4 and Figure 5 respectively.

Figure 4: HU vs. ED_r at various kVp.

Tissue Equivalent Material	HU Recorded (80 kVp)	HU Recorded (100 kVp)	HU Recorded (120 kVp)	HU Recorded (140 kVp)
Lung Inhale	-759.45	-760.92	-763.09	-763.71
Lung Exhale	-476.97	-478.89	-479.51	-480.07
Adipose	-76.86	-66.46	-60.65	-55.65
Breast (50% gland/ 50% Adipose)	-30.40	-24.67	-22.33	-19.57
Muscle	55.6	55.19	53.14	53.82
Liver	71.51	69.86	68.65	68.53
Solid Trabecular Bone (200 mg/cc HA)	374.15	309.05	253.8	216.07
Solid Dense Bone (800 mg/cc HA)	1361.94	1133.37	976.15	882.24